题目描述
给定两个由一些闭区间组成的列表,每个区间列表都是成对不相交的,并且已经排序。返回这两个区间列表的交集。
(形式上,闭区间 [a, b](其中 a <= b)表示实数 x 的集合,而 a <= x <= b。两个闭区间的交集是一组实数,要么为空集,要么为闭区间。例如,[1, 3] 和 [2, 4] 的交集为 [2, 3]。)
示例:
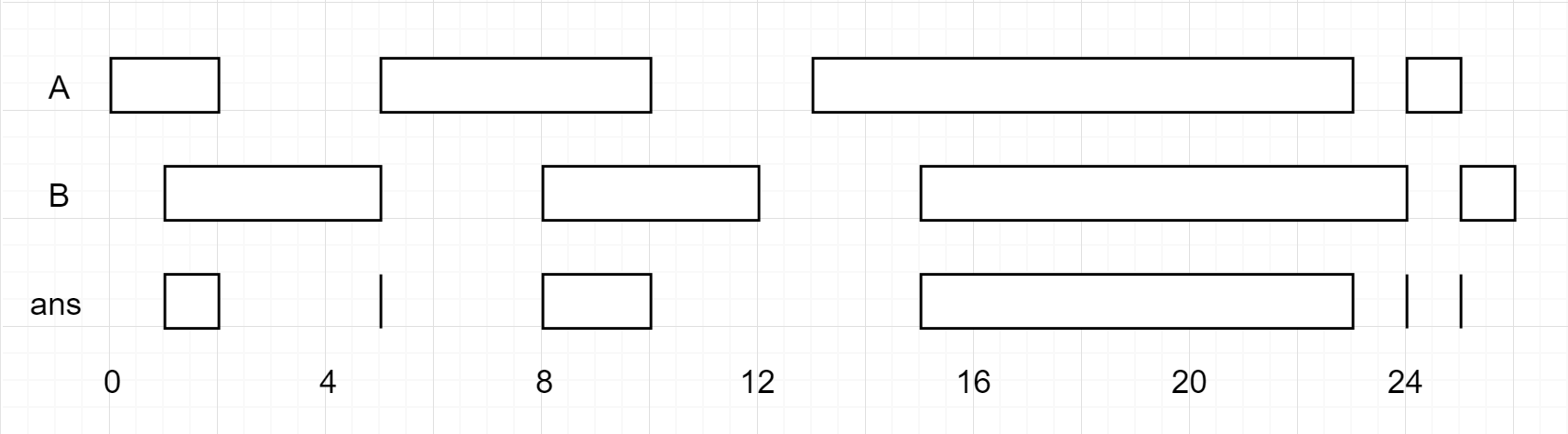
输入:A = [[0, 2], [5, 10], [13, 23], [24, 25]], B = [[1, 5], [8, 12], [15, 24], [25, 26]]
输出:[[1, 2], [5, 5], [8, 10], [15, 23], [24, 24], [25, 25]]
提示:
- 0 <= A.length < 1000
- 0 <= B.length < 1000
- 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9
题解
最开始我的想法是使用一个指针 start 扫描两个闭区间的值,判断当前 start 的值是否在 A[indexA] 和 B[indexB] 的区间内,发现进入到区间后,那么我们再引入 end 指针,值为 start 的值,然后移动 end 指针,直到出了 A[indexA] 或者 B[indexB] 的区间范围,那么 start 和 end - 1 的值就是两个区间的交集。然后将 end 的值赋值给 start 并判断 start ,如果超出了 A[indexA] 或者 B[indexB] 的区间,则分别进行 indexA++ 或者 indexB++ 的操作。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| public int[][] intervalIntersection(int[][] A, int[][] B) {
if (A == null || B == null) {
return new int[0][];
}
List<int[]> ans = new ArrayList<>();
int indexA = 0;
int indexB = 0;
int start = 0;
int[] common = new int[2];
while (indexA < A.length && indexB < B.length) {
if (A[indexA][0] <= start && start <= A[indexA][1] && B[indexB][0] <= start && start <= B[indexB][1]) {
common[0] = start;
int end = start;
while (A[indexA][0] <= end && end <= A[indexA][1] && B[indexB][0] <= end && end <= B[indexB][1]) {
end++;
}
common[1] = end - 1;
ans.add(common.clone());
start = end;
} else {
start++;
}
if (start > A[indexA][1]) {
indexA++;
}
if (start > B[indexB][1]) {
indexB++;
}
}
return ans.toArray(new int[0][]);
}
|
上面的方法在提交后超时了,分析用例和代码发现,上面的代码有以下两个问题:
- start 的值从 0 开始,如果 A[0] 和 B[0] 的起始值比较大,那么就做了很多无用的
start++ 操作。
- end 的值从 start 开始,遍历到区间的最大值,如果区间范围过大,也会导致频繁的
end++。
于是我们根据上面的问题进行优化,先从 A[0] 和 B[0] 开始找规律,假设两个闭区间有交集,那么我们可以发现,交集的起始值 start = max(A[0][0], B[0][0]),交集的终止值 end = min(A[0][1], B[0][1])。这样我们相比上面的方法,减少了很多无用的 ++ 操作。延申而来,对于任意的 A[indexA] 和 B[indexB] 都可以这样求出交集。但是如果求出 start > end 则认为这两个区间没有交集,然后我们对于提前结束的集合,即集合的最大值等于 end 的集合,我们对其指针进行 index++ 操作。因为较早结束的集合,已经计算完交集了,而另外一个范围比较大的集合,还有有值没有计算是否相交。下面看代码将会更好的理解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public int[][] intervalIntersection(int[][] A, int[][] B) {
if (A == null || B == null) {
return new int[0][];
}
List<int[]> ans = new ArrayList<>();
int indexA = 0;
int indexB = 0;
while (indexA < A.length && indexB < B.length) {
int start = Math.max(A[indexA][0], B[indexB][0]);
int end = Math.min(A[indexA][1], B[indexB][1]);
if (start <= end) {
ans.add(new int[]{start, end});
}
if (A[indexA][1] == end) {
indexA++;
}
if (B[indexB][1] == end) {
indexB++;
}
}
return ans.toArray(new int[0][]);
}
|
进一步我们使用条件运算符优化下 16 行开始的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public int[][] intervalIntersection(int[][] A, int[][] B) {
if (A == null || B == null) {
return new int[0][];
}
List<int[]> ans = new ArrayList<>();
int indexA = 0;
int indexB = 0;
while (indexA < A.length && indexB < B.length) {
int start = Math.max(A[indexA][0], B[indexB][0]);
int end = A[indexA][1] < B[indexB][1] ? A[indexA++][1] : B[indexB++][1];
if (start <= end) {
ans.add(new int[]{start, end});
}
}
return ans.toArray(new int[0][]);
}
|
复杂度分析
- 时间复杂度:O(M + N),其中 M, N 分别是数组 A 和 B 的长度。
- 空间复杂度:O(M + N),答案中区间数量的上限。
来源
区间列表的交集 | 力扣(LeetCode)
区间列表的交集 | 题解(LeetCode)


