题目描述

给定范围 [m, n]，其中 0 <= m <= n <= 2147483647，返回此范围内所有数字的按位与（包含 m, n 两端点）。

示例 1:

输入: [5, 7]
输出: 4

示例 2:

输入: [0, 1]
输出: 0

题解

我们观察按位与运算的性质。对于一系列的位，例如 [1, 1, 0, 1, 1]，只要有一个零的位，那么这一系列位的按位与运算结果都将为零。对于此题，我们将一系列数字变成二进制展示，如下：

-	4	5	6	7	8
0	0	0	0	0	0
1	0	0	0	0	1
2	0	0	0	1	0
3	0	0	0	1	1
4	0	0	1	0	0
5	0	0	1	0	1
6	0	0	1	1	0
7	0	0	1	1	1
8	0	1	0	0	0
9	0	1	0	0	1
10	0	1	0	1	0
11	0	1	0	1	1
12	0	1	1	0	0
13	0	1	1	0	1
14	0	1	1	1	0
15	0	1	1	1	1
16	1	0	0	0	0

上面表格中，我将[0, 16] 全部展开成8进制展示，上图中，我们任意取出一个范围，比如[9, 12]，我们可以发现，对所有数字执行按位与运算的结果是所有对应二进制字符串的公共前缀再用零补上后面的剩余位。那么这个规律是否正确呢？我们可以进行简单的证明。假设对于所有这些二进制串，前 i 位均相同，第 i + 1 位开始不同，由于 [m, n] 连续，所以第 i + 1 位在 [m, n] 的数字范围从小到大列举出来一定是前面全部是 0，后面全部是 1，在上图中对应 [9, 11] 均为 0，[12, 12] 均为 1。并且一定存在连续的两个数 x 和 x + 1，满足 x 的第 i + 1 位为 0，后面全为 1，x + 1 的第 i + 1 位为 1，后面全为 0，对应上图中的例子即为 11 和 12。这种形如 0111… 和 1000… 的二进制串的按位与的结果一定为 0000…，因此第 i + 1 位开始的剩余位均为 0，前 i 位由于均相同，因此按位与结果不变。最后的答案即为二进制字符串的公共前缀再用零补上后面的剩余位。

进一步来说，所有这些二进制字符串的公共前缀也即指定范围的起始和结束数字 m 和 n 的公共前缀（即在上面的示例中分别为 9 和 12）。因此，最终我们可以将问题重新表述为：给定两个整数，我们要找到它们对应的二进制字符串的公共前缀。

位移操作

我们的想法是将两个数字不断向右移动，直到数字相等，即数字被缩减为它们的公共前缀。计算移动的次数，然后，通过将公共前缀向左移动相同次数，将零添加到公共前缀的右边以获得最终结果。

public int rangeBitwiseAnd(int m, int n) {
    int count = 0;
    while (m != n) {
        m = m >> 1;
        n = n >> 1;
        count++;
    }
    return m << count;
}

复杂度分析

时间复杂度：O(logn)。算法的时间复杂度取决于 m 和 n 的二进制位数，由于 m ≤ n，因此时间复杂度取决于 n 的二进制位数。
空间复杂度：O(1)。我们只需要常数空间存放若干变量。

Brian Kernighan 算法

还有一个位移相关的算法叫做「Brian Kernighan 算法」，它用于清除二进制串中最右边的 1。Brian Kernighan 算法的关键在于我们每次对 n 和 n − 1 之间进行按位与运算后，n 中最右边的 1 会被抹去变成 0。

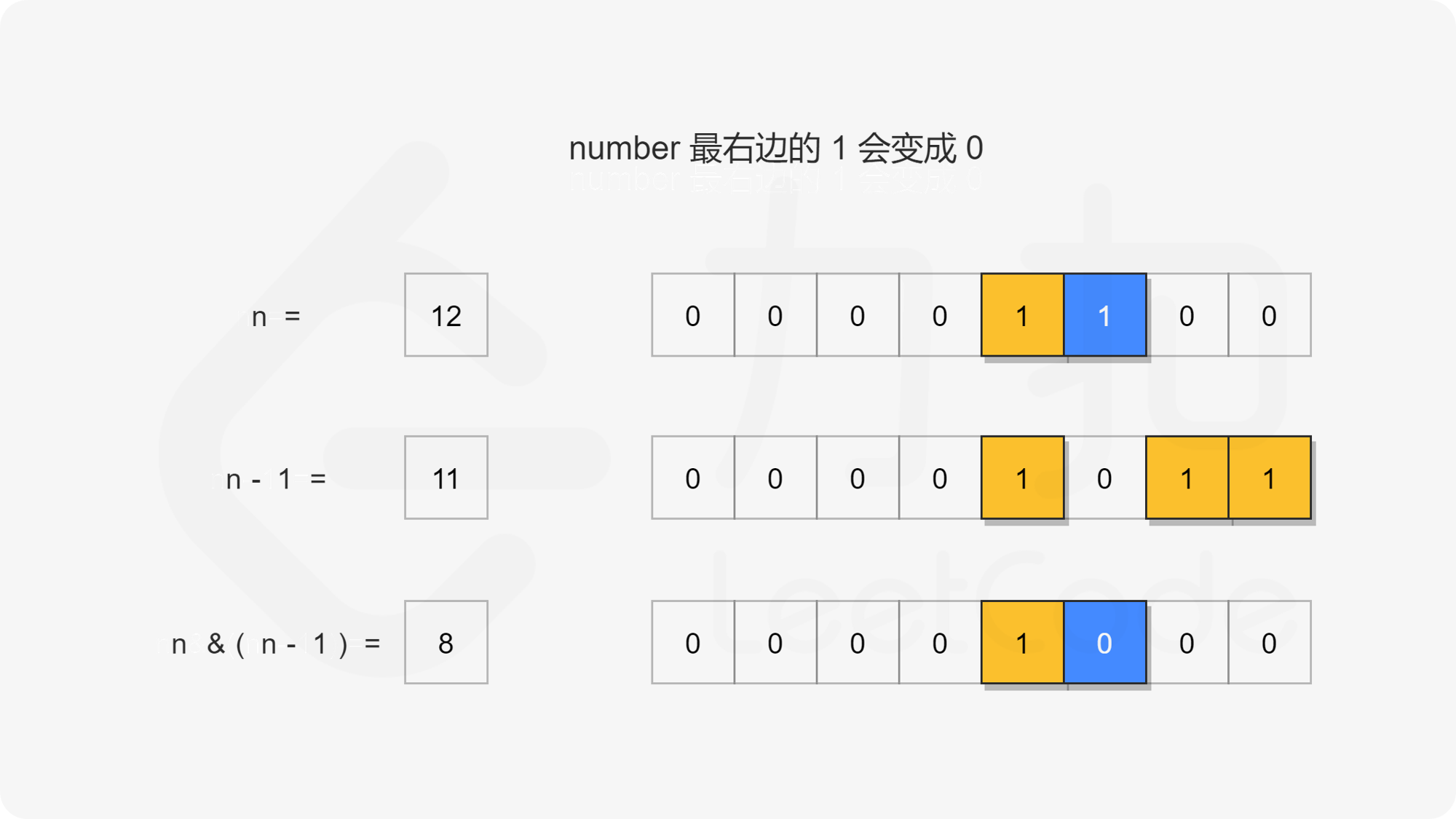
基于上述技巧，我们可以用它来计算两个二进制字符串的公共前缀。其思想是，对于给定的范围 [m, n]（m < n），我们可以对数字 n 迭代地应用上述技巧，清除最右边的 1，直到它小于或等于 m，此时非公共前缀部分的 1 均被消去。因此最后我们返回 n 即可。

public int rangeBitwiseAnd(int m, int n) {
    while (m < n) {
        n = n & (n - 1);
    }
    return n;
}

复杂度分析

时间复杂度：O(logn)。和位移方法类似，算法的时间复杂度取决于 m 和 n 二进制展开的位数。尽管和位移方法具有相同的渐近复杂度，但 Brian Kernighan 的算法需要的迭代次数会更少，因为它跳过了两个数字之间的所有零位。
空间复杂度：O(1)。我们只需要常数空间存放若干变量。

来源

数字范围按位与 | 力扣（LeetCode）
数字范围按位与 | 题解（LeetCode）

-	4	5	6	7	8
0	0	0	0	0	0
1	0	0	0	0	1
2	0	0	0	1	0
3	0	0	0	1	1
4	0	0	1	0	0
5	0	0	1	0	1
6	0	0	1	1	0
7	0	0	1	1	1
8	0	1	0	0	0
9	0	1	0	0	1
10	0	1	0	1	0
11	0	1	0	1	1
12	0	1	1	0	0
13	0	1	1	0	1
14	0	1	1	1	0
15	0	1	1	1	1
16	1	0	0	0	0

-	4	5	6	7	8
0	0	0	0	0	0
1	0	0	0	0	1
2	0	0	0	1	0
3	0	0	0	1	1
4	0	0	1	0	0
5	0	0	1	0	1
6	0	0	1	1	0
7	0	0	1	1	1
8	0	1	0	0	0
9	0	1	0	0	1
10	0	1	0	1	0
11	0	1	0	1	1
12	0	1	1	0	0
13	0	1	1	0	1
14	0	1	1	1	0
15	0	1	1	1	1
16	1	0	0	0	0

-	4	5	6	7	8
0	0	0	0	0	0
1	0	0	0	0	1
2	0	0	0	1	0
3	0	0	0	1	1
4	0	0	1	0	0
5	0	0	1	0	1
6	0	0	1	1	0
7	0	0	1	1	1
8	0	1	0	0	0
9	0	1	0	0	1
10	0	1	0	1	0
11	0	1	0	1	1
12	0	1	1	0	0
13	0	1	1	0	1
14	0	1	1	1	0
15	0	1	1	1	1
16	1	0	0	0	0